# Analysis of SpaceX's Crewed Dragon Launch: A Physics Perspective
Written on
Chapter 1: The Significance of the Launch
The recent launch of SpaceX's Crewed Dragon 2 into orbit, successfully docking with the International Space Station, marks a pivotal moment in space exploration. Since its founding in 2002, SpaceX has achieved remarkable milestones, including its first orbital rocket, Falcon 1, in 2008. Notably, the USA has not seen a crewed spacecraft since the 2011 launch of the space shuttle Atlantis.
So, how should one commemorate such an event? While some might compose a song or create artwork, my method involves delving into physics. Today, I will conduct a video analysis of the launch to calculate the rocket’s acceleration. If you missed the launch, here's a brief recap.
Chapter 2: Launch Analysis Techniques
The initial phase of the launch provides the best data for analysis. The objective is to determine the spacecraft's vertical position over time. To achieve this, I plan to utilize Tracker Video Analysis—an excellent free software—to pinpoint the rocket's position in each video frame. However, with the camera moving and zooming, establishing a reference point is crucial for correlating video pixels with actual distances. The launch tower serves as a useful reference, but once the rocket ascends beyond it, the context diminishes.
Before diving into data collection, it’s essential to clarify the rocket's dimensions. According to Spaceflight Insider, the Falcon 9 measures 41.2 meters in length, extending to 47.7 meters with the interstage. However, this does not account for the Dragon 2 spacecraft itself. The height of the Falcon 9, verified at 47.7 meters, provides a reliable measurement.

The challenge lies in using the water tower and launch tower as reference points. Given their different distances from the camera, there may be perspective errors. Still, I believe this can be mitigated due to the camera's positioning. To demonstrate the effectiveness of calibration points, here is a corrected view from the video analysis.

This analysis yields the following position versus time graph for the rocket:
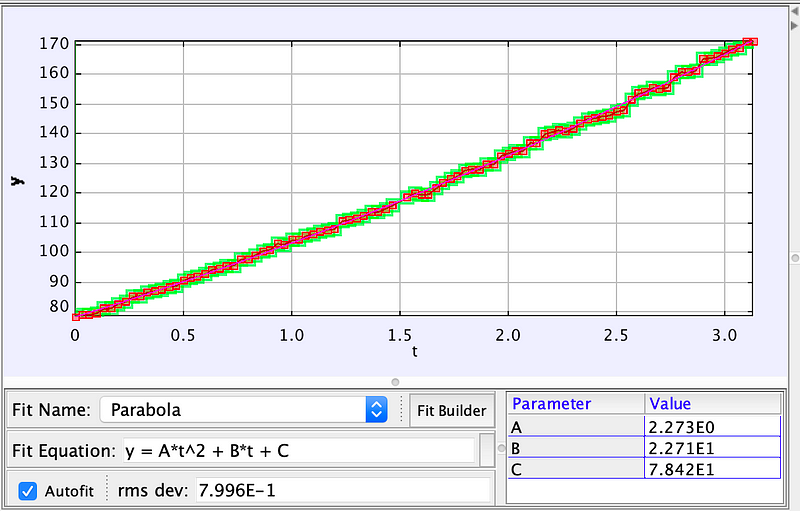
Using the assumption of constant acceleration, I can apply a quadratic function to fit the data, allowing me to calculate the acceleration. The relevant kinematic equation for one-dimensional motion under constant acceleration is as follows:
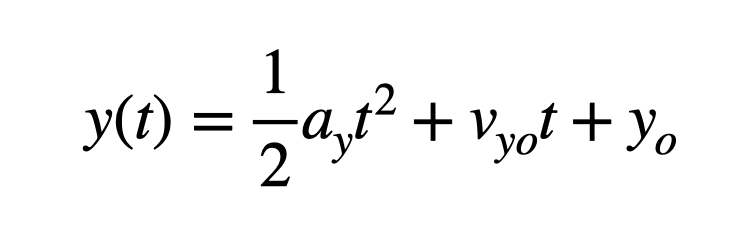
The coefficient associated with the t² term represents half of the acceleration. By doubling this coefficient, I determine that the acceleration of the Dragon 2 rocket is approximately 4.5 m/s². This is the figure I was seeking.
What does this acceleration translate to in terms of "g's"? Standing on solid ground, one experiences 1 g. Thus, this acceleration equates to about 0.46 g's (4.5/9.8), resulting in a total of 1.46 g's when factoring in gravitational force. In comparison, the space shuttle experienced around 3 g's during its launch. While I remain unsure of the absolute accuracy of my findings, I am content with this estimate.
Now, let's consider the acceleration during the later stages of the launch. I will reference the SpaceX velocity display featured in the video (assuming its accuracy). This data yields the following insights.
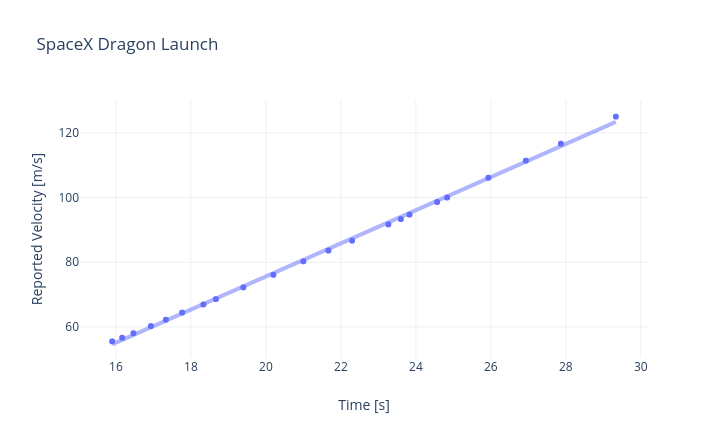
I converted the velocity from km/h to m/s, revealing a linear change in velocity, indicative of constant acceleration. The slope of this line corresponds to an acceleration value of 5.12 m/s², which is reasonably close to my earlier estimate. However, it’s important to note that the rocket will not maintain constant acceleration throughout its flight. As it ascends to higher altitudes, air resistance decreases and the rocket's mass diminishes due to fuel consumption.
To wrap up, here are a couple of questions for you to ponder:
- Calculate the mass of the fully-loaded rocket and the thrust force generated by the Falcon 9. Use this data to estimate the lift-off acceleration.
- Track the velocity versus time for the remainder of the flight. Does the acceleration vary significantly?