Finding Sphere Volume Using Calculus Techniques
Written on
Understanding Solids of Revolution
Calculating the volume of a sphere with radius r can be achieved using calculus techniques. Although one might think that a double or triple integral is required for a three-dimensional shape, it turns out that a single integral is sufficient for this task.
Before diving into the specifics of the sphere, we need to familiarize ourselves with the concept of solids of revolution. The volume of such solids can be determined by rotating a standard integral around an axis.
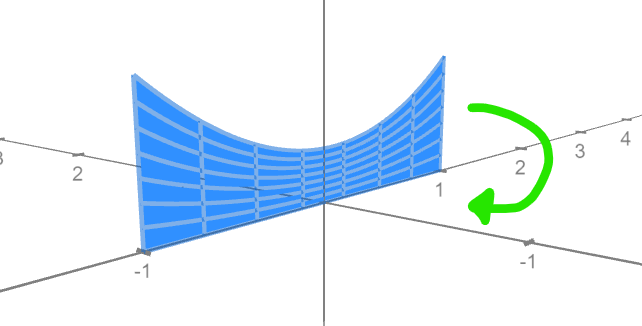
We can visualize the integral prior to rotation, as shown in the image above.
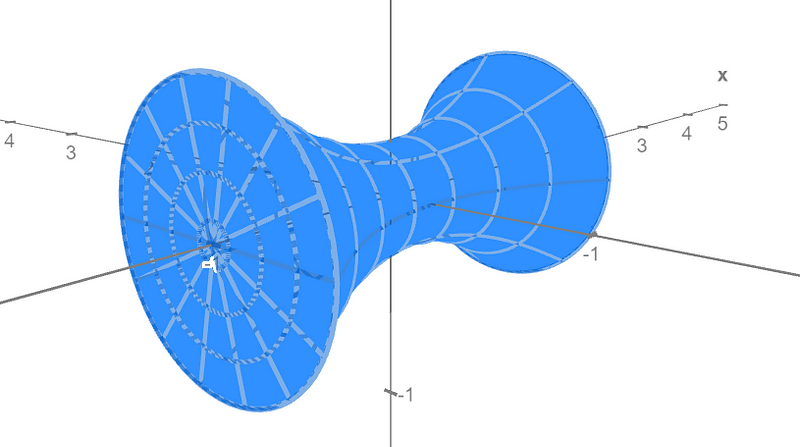
The image illustrates the solid formed by the rotation of the integral.
To better understand the process, we can think of constructing a standard integral by summing up the areas of rectangles that gradually become thinner, thus better approximating the area beneath the curve. This is the fundamental idea behind the Riemann integral.
When it comes to calculating the volume of a solid of revolution, we can sum the volumes of increasingly thin cylinders instead. Let’s denote the function defining the curve we rotate around the x-axis as f(x). In the case of a standard Riemann integral, the area of each rectangle starting at x can be expressed as f(x) * dx, where dx represents the width.
Take a look at the thin cylinder depicted below:
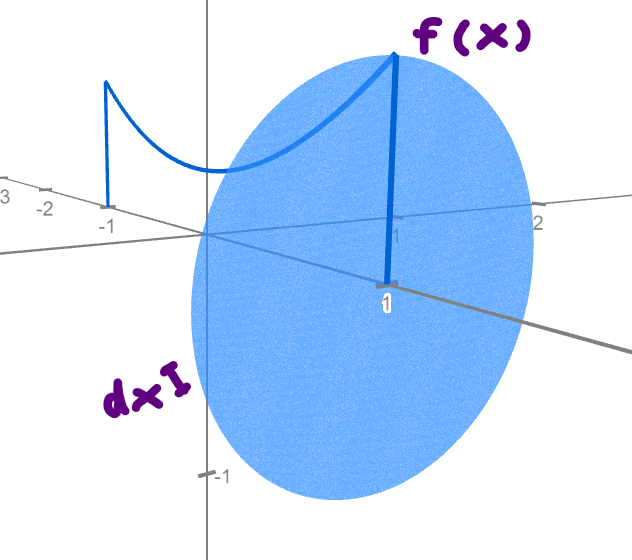
In this illustration, the volume of the cylinder is calculated as ( pi * r² * h ). Here, h represents the small width of the cylinder along the x-axis, denoted as dx. The radius corresponds to the length of the dark blue line within the cylinder, which is f(x). For this particular cylinder, it is f(1) since it starts at 1 on the x-axis.
Thus, the volume of each thin cylinder can be expressed as ( pi * f(x)² * dx ).
Similar to how we sum the areas of rectangles with an integral to find the area beneath a curve, we can sum the volumes of these cylinders with an integral as follows:
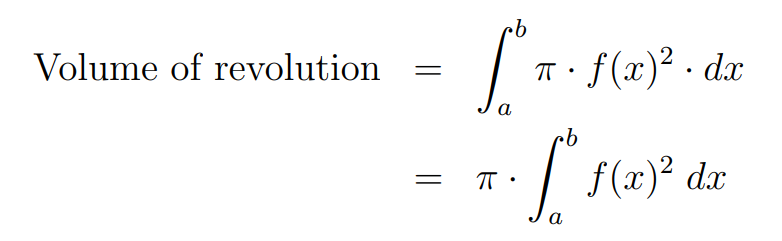
In this formula, [a, b] indicates the interval where the function f(x) is defined.
Calculating the Volume of a Sphere
Now that we have a grasp of how to compute volumes of revolution, let’s apply this knowledge to find the volume of a sphere with radius r. We achieve this by rotating a semicircle around the x-axis.
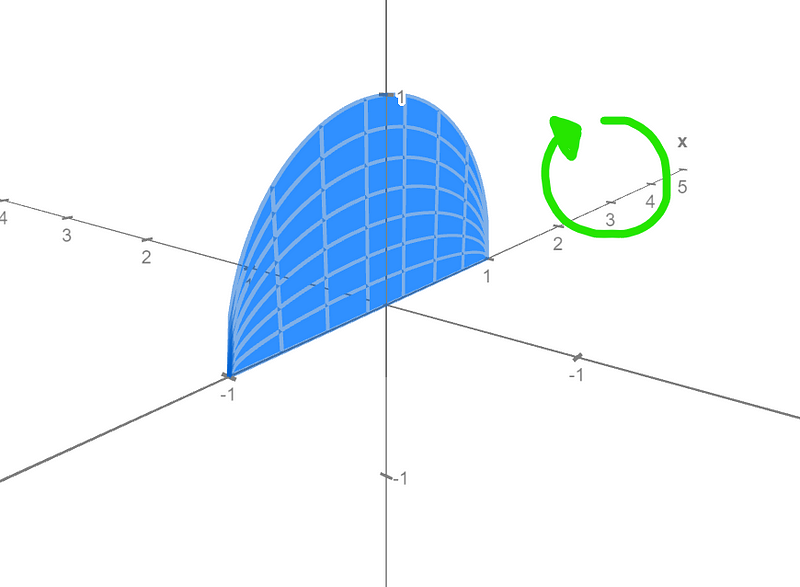
The boundary of the semicircle is defined by the function f(x) = √(r² — x²), which is valid on the interval [-r, r].
With all the components in place, we can now calculate the volume of the sphere. Let's enjoy the calculations!
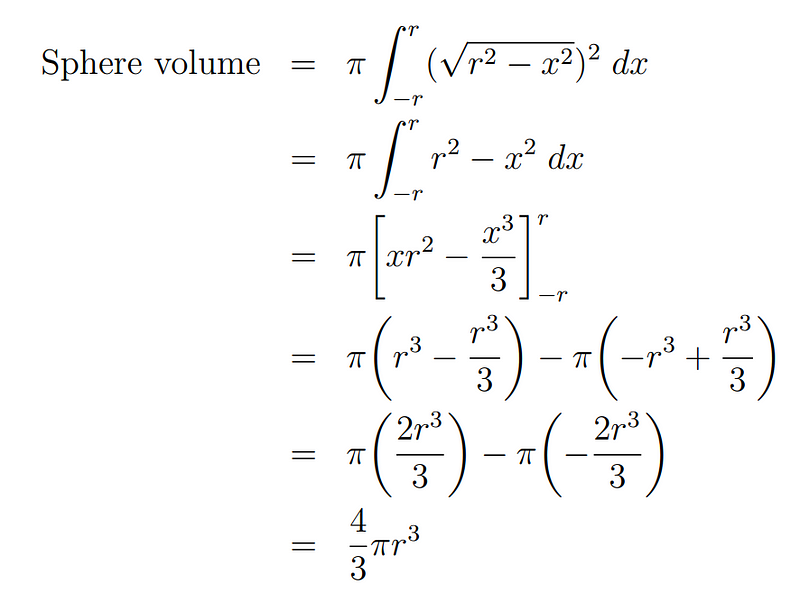
This calculation leads us to the well-known formula for the volume of a sphere: ( frac{4}{3} pi r³ ).

Applications of Volumes of Revolution
By utilizing the concept of volumes of revolution, you can determine the volume of any object that can be shaped on a pottery wheel, as long as the side view of your pottery is square-integrable! Additionally, you can derive the volume of a cylinder by letting f(x) be a constant function, resulting in a cylinder when rotated around the x-axis. Consider giving it a try!
Exploring the Volume of Spheres with Video Tutorials
To enhance your understanding of these concepts, check out these informative video tutorials:
The first video titled Find the Volume of Spheres using Integral Calculus explains the process in detail:
The second video, Derive the Volume of a Sphere Using Integration (Disk Method), delves deeper into the integration techniques used to derive the volume: