Colorful Geometry: Discovering the Red Fraction in Dodecagons
Written on
Chapter 1: Understanding the Problem
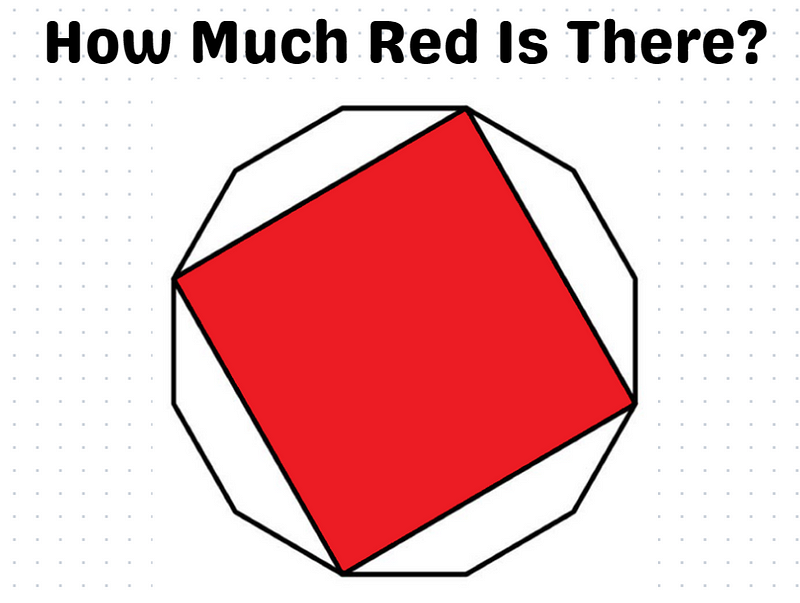
The red square is formed using the vertices of a regular dodecagon, as illustrated. Our goal is to determine what portion of the dodecagon is shaded in red.
To provide a captivating solution, I encourage you to pause here, gather your pen and paper, and attempt the problem before continuing!
Solution
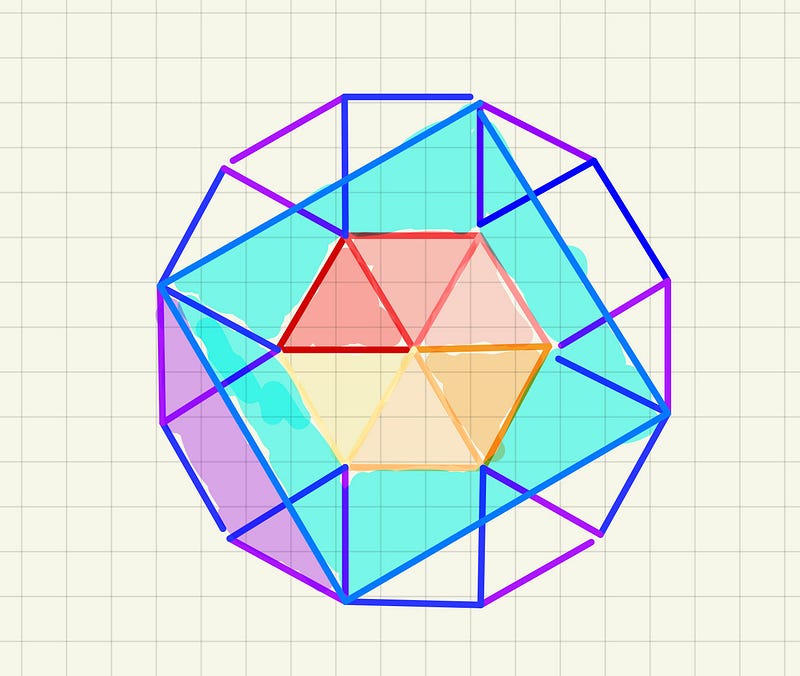
I have divided the figure into six squares along the edges, six triangles within the central hexagon, and six additional triangles surrounding it.
Take note of the purple region! It consists of half a square and two half-triangles:
[ ? = frac{1}{2}? + ? ]
The entire hexagon can be expressed as:
[ ? = 6? + 12? ]
By subtracting four times the purple region, we arrive at:
What remains is:
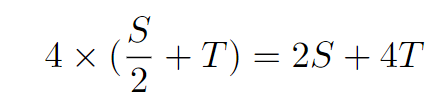
This can be simplified to:
[ 4? + 8? = frac{2}{3}(6? + 12?) ]
Thus, the answer reveals that ( frac{2}{3} ) of the entire dodecagon is shaded in red! Isn’t that fascinating?
What was your approach to this problem? I would love to hear your thoughts in the comments below!
Math Puzzles
For those interested, here’s a collection of some of the finest math puzzles available on Medium, covering topics like Algebra, Geometry, Calculus, and Number Theory. Feel free to share this with your friends!
The first video titled "What fraction of the colors is red?" elaborates on the fascinating interplay of colors in geometric shapes.
Get notified whenever I publish new content. Thank you for your support!
The second video provides a detailed summary of the distribution of color and shape among 100 tiles of equal area, enhancing our understanding of geometric proportions.
Thank you for your time! If you found this article helpful, please give it a clap!
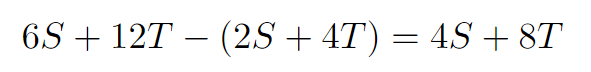
If you feel inclined to support my work, consider buying me a coffee. Your generosity goes a long way in helping me continue my writing and academic journey.
Happy Solving, Bella 😊