Chapter 1: The Nature of Mathematical Formulas

In the realm of viral content, some videos captivate audiences by posing what appear to be trivial questions. However, the inquiries discussed here are anything but trivial. They are, in fact, profound. Many have already weighed in on these topics, but I will share my perspectives, thanks to Gracie for her thought-provoking questions.

Let’s delve into the first inquiry: how do mathematicians derive various formulas? For example, consider the formula for the circumference of a circle.

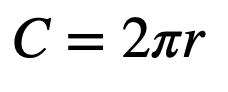
This formula indicates that the distance around a circle is related to its radius. Additionally, it includes the essential constant π. This principle was likely recognized by ancient civilizations, such as the Babylonians and Egyptians. They viewed it not merely as an equation but as a fundamental concept: the relationship that the circumference is proportional to the diameter, regardless of the circle's size. Interestingly, these early mathematicians did not possess an exact value for π.

Through their exploration, they identified this relationship. What about other formulas? A notable example is Maxwell’s Equations in physics, which articulate the connection between electric and magnetic fields. These equations not only describe these fields but also reveal that they propagate as waves, leading to the discovery of electromagnetic waves that travel at light's speed.

Returning to the initial query: did mathematicians know precisely what they sought? Sometimes they did, often driven by the necessity to solve practical problems. Other times, their pursuits were more experimental and playful.

Section 1.1: Validating Mathematical Formulas

One fundamental aspect of science, as opposed to philosophy, is experimentation. Let’s shift the focus back to science, even though the primary discussion revolves around mathematics.

In scientific inquiry, we construct models and subject them to real-world testing. These models can take various forms, including mathematical equations or conceptual frameworks. Without empirical validation, a model remains speculative.

Take, for instance, the equation for the circumference of a circle. Although straightforward, one can easily conduct a simple experiment using a string to measure the circumference and the diameter of actual circles. If the ratio of circumference to diameter remains constant across various circles, the formula holds true.

However, some relationships, such as Euler's Identity, are more complex.

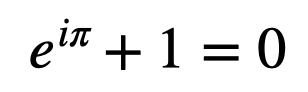
This identity links the natural number e, π, and the imaginary unit i. Demonstrating this concept through tangible measurements is challenging, yet it is a valid mathematical relationship, frequently appearing in quantum mechanics and wave theory.

Does this validate its correctness? Not necessarily. It demonstrates functionality, but the absolute truth remains elusive.

Chapter 2: The Importance of Inquiry

The first video, "Always Get These Math Questions CORRECT– Must Know For All Test Takers!" explores key strategies for mastering math questions essential for standardized tests.

The second video, "Answer These 15 ACT Math Problems to Score a 30+ on ACT Math," presents crucial problems that can elevate your ACT Math score.

Moving on to another question: why did a physicist, followed by a prominent figure like Barack Obama, retweet Gracie's questions? The retweet likely reflects her ability to engage in deeper thought, which resonates with many, including myself.

In closing, thank you, Gracie, for your insightful questions. While they may not have been directed at me, I thoroughly enjoyed addressing them.