Exploring the Geometry of Rhombuses: A Puzzling Challenge
Written on
Chapter 1: The Geometry Puzzle
In this intriguing geometry challenge, we will delve into the properties of rhombuses nestled within squares. The diagram illustrates two distinct shaded rhombuses, each placed inside a square with side lengths of 6. These rhombuses are created by connecting the vertices of the square to the midpoints of its sides. The question arises: what is the difference in the areas of these shaded shapes? To get started, consider drawing some lines for clarity.
I encourage you to take a moment to pause here, grab a pen and paper, and attempt the puzzle before moving on to the solution.
Solution Overview
Let’s begin by adding some lines to the square on the left side of our diagram.
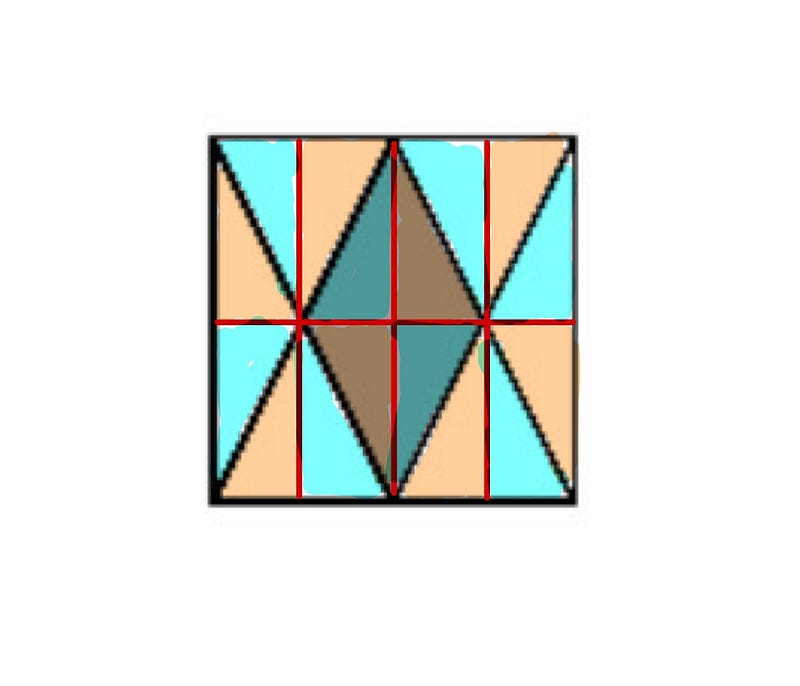
The three vertical lines depicted in red are evenly spaced. Additionally, the horizontal line in red bisects the square. This configuration divides the square into 16 congruent triangles, 4 of which form the rhombus.
With the side length of the square being 6, and knowing that the rhombus occupies 4 out of the 16 triangles, we can determine the area of the rhombus.
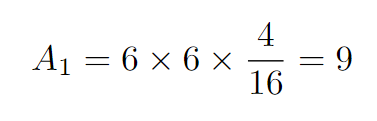
We have labeled the area of the first rhombus as A1. If you have yet to arrive at a solution, here’s another opportunity to pause the article and apply similar reasoning to the second square. Consider drawing lines again!
Analyzing the Second Rhombus
The key to understanding the second figure is to draw a diagonal from the top left corner to the bottom right corner of the square.
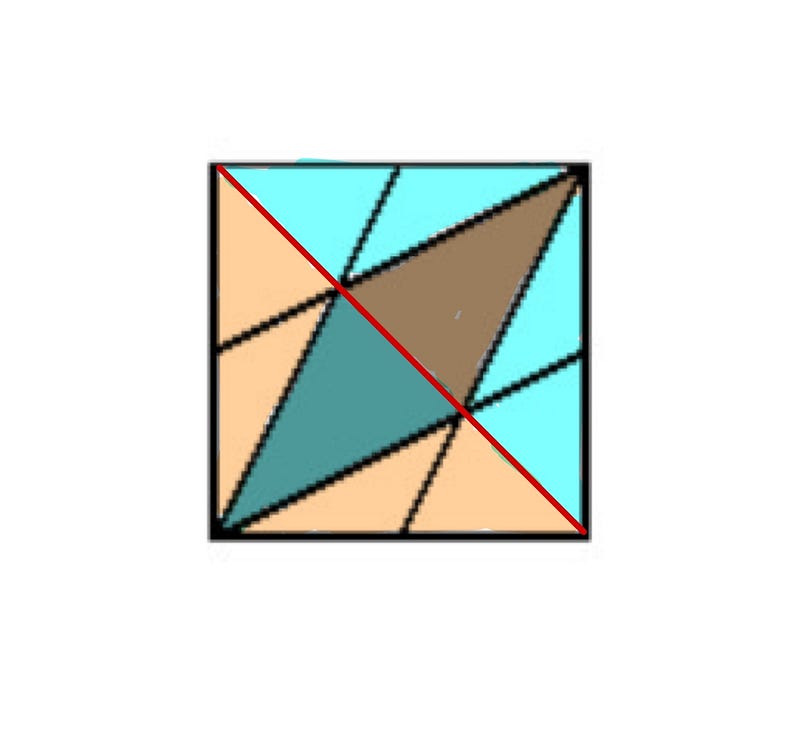
The red diagonal divides the square into two equal halves, where each half consists of three triangles of equal area. How can we be certain they possess equal areas? Each triangle’s base divides the diagonal into three equal segments, and they all share the same height.
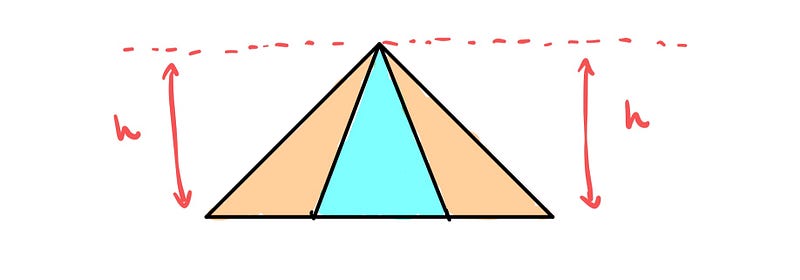
This results in the entire square being composed of six triangles with identical areas. Thus, if 6A = 24, we find A = 4. Consequently, the area of each triangle is 4. The squashed rhombus in the second square comprises two of these triangles, giving it an area of:
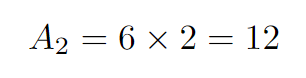
Ultimately, the difference in areas between the two rhombuses is:
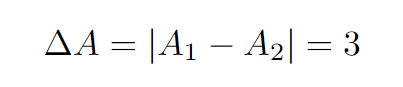
And there you have it—our answer! Isn’t it fascinating?
Reflection and Engagement
What were your thoughts during this exercise? I invite you to share your reflections in the comments below; I would love to hear from you!
The first video titled "Constructing a Rhombus" provides a visual demonstration of how to create rhombuses within squares, which complements our discussion beautifully.
The second video, "11.4.2 How do you find the area of a rhombus?" dives deeper into the area calculations for rhombuses, further enriching your understanding.
Thank you for engaging with this puzzle! If you enjoyed this content, please consider supporting my work by visiting my Ko-fi page. Your support allows me to continue sharing these intriguing math challenges with you.
Happy Solving, Bella