Chapter 1: The Unassuming 1729

The number 1729 may seem ordinary at first glance, but it carries a remarkable story within the realm of mathematics. In 1918, the renowned British mathematician G. H. Hardy visited his ailing colleague, Srinivasa Ramanujan, in a London hospital. During this visit, Hardy mentioned that he had taken a taxi numbered 1729, remarking that it was not particularly noteworthy.

However, Ramanujan countered this claim by revealing an astonishing fact about 1729: it is the smallest number expressible as the sum of two cubes in two distinct ways.

This unique property makes 1729 quite special. For example, it can be represented as:

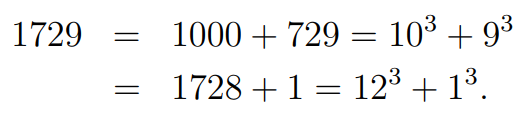
Additionally, another intriguing number that can also be expressed as the sum of two cubes in two different forms is:

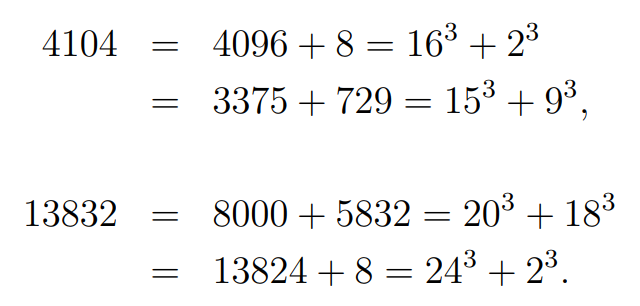
It's noteworthy that 13832 can be derived from multiplying 1729 by (2^3). Repeatedly applying this idea with any cube yields an endless series of numbers that can similarly be expressed as sums of two cubes in two distinct manners.

Naturally, a question arises: are there numbers that can be represented as the sum of two cubes in three or even four different ways? The answer is affirmative. In 1938, G. H. Hardy and E. M. Wright proved that for every positive integer ( n ), there exists a number that can be expressed as the sum of two cubes in ( n ) different ways. While there are constructive proofs for this, the smallest such numbers produced are not necessarily the smallest overall.

The smallest number expressible as a sum of two cubes in ( n ) different ways is referred to as the ( n )-th taxicab number. The first six of these numbers are well-documented.

For brevity, the various cubic decompositions of these taxicab numbers are linked here. Beyond the sixth, we only have upper bounds available. Finding a number that fits the criteria provides an upper limit, and the current upper bound for Taxicab(7) is noted as follows:

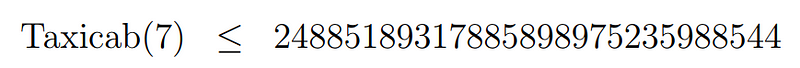
The exploration of these impressive numbers was all sparked by Hardy's taxi experience in 1918. It's fascinating to see how Hardy himself contributed further to the research on taxicab numbers, a field that continues to evolve today.

The first video delves into the story of the Hardy-Ramanujan number 1729, illustrating its significance in the world of mathematics.

The second video explores why 1729 is considered a special number, showcasing its unique characteristics and the magic behind it.

Exercise: Can you find a number that can be expressed as the sum of two squares in two different ways?