Discover the Joy of Perfect Squares: A Fun Math Challenge
Written on
Chapter 1: Introduction to Perfect Squares
Even as a university math student, I find that there is often an excessive level of complexity in academic environments. Lecture materials frequently contain intricate phrases filled with specialized terminology.
Through this blog, I aim to offer a more enjoyable way to explore the elegance of mathematics, enabling individuals from various backgrounds to strengthen their cognitive skills, one puzzle at a time. ✨
To clarify, n! denotes n factorial, which is defined as n! = (n)(n-1)...(2)(1). I encourage you to pause here, grab some paper and a pen, and give this puzzle a try before you continue on for the solution! 🧠
Section 1.1: Understanding the Puzzle
Take a moment to observe that the denominator in each term is created by multiplying two successive factorials, such as (14!)(15!) and (15!)(16!).
A logical method to tackle this puzzle involves articulating the general structure of these terms.

We can adjust the expression by noting that:
(n + 1)! = (n + 1)n!
Reintroducing this into the expression results in:

At this point, we see that our expression is a combination of a squared term, (n!)², and a fraction, (n + 1)/2.
So, how do we transform the term into a perfect square? 🧐
Recall that (ab)² = a²b², indicating that the expression is a perfect square if and only if (n + 1)/2 is a perfect square itself!
Section 1.2: Finding the Perfect Square
Now, we simply need to calculate (n + 1)/2, where n corresponds to the smaller factorial in each fraction!
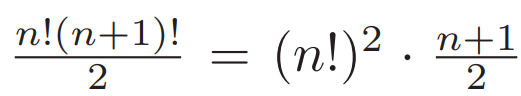
In this case, we find that 9 = 3²!
Thus, (17!)(18!)/2 becomes our perfect square solution!
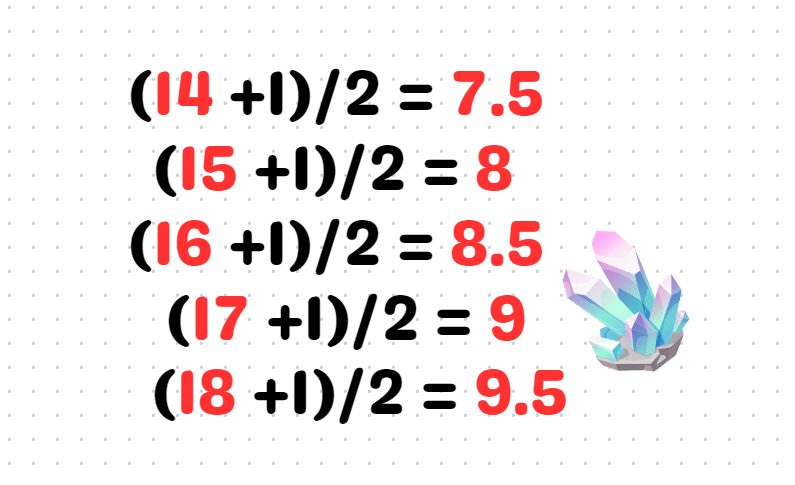
What an incredible journey! 🌟
What were your thoughts while working through this puzzle? Please share your insights in the comments; I'm excited to hear from you!
Chapter 2: Exploring More Math Challenges
If you enjoyed this puzzle, consider checking out a compilation of the best math challenges available on Medium.
Math Puzzles
A curated selection of intriguing math puzzles covering Algebra, Geometry, Calculus, Number Theory, and beyond.
Feel free to share this with friends and fellow math enthusiasts!
Thank you for taking the time to read this. If you found the content valuable, please show your support by clapping for the article. Your encouragement means a lot!

If you're feeling generous, consider buying me a coffee to support my writing efforts. Your contribution helps me in both my personal and academic pursuits.
With gratitude, Bella 💖