Chapter 1: Introduction to Differentiation Rules

In the realm of calculus, the sum rule and difference rule stand as essential methods for differentiating combinations of functions. This marks the eighth installment in our calculus series, where we have previously focused on simpler algebraic expressions. Now, we will advance to differentiating more intricate functions that are formed by adding or subtracting simpler components.

Understanding a Function as a Sum of Simpler Functions

Consider two functions, ‘u’ and ‘v’, both dependent on ‘x’, along with ‘y’ defined as follows:

u = f(x)

v = f(x)

y = f(x) = u + v

To differentiate ‘y’ with respect to ‘x’, one might ponder whether to differentiate ‘u’ and ‘v’ individually and then add the results. Spoiler alert: that’s exactly what the sum rule of calculus instructs us to do. However, it’s crucial to formalize this process to grasp the underlying principles justifying the sum rule's validity.

Let’s recall from earlier discussions that if we increase ‘x’ by an infinitesimal increment ‘dx’, then ‘y’ increases correspondingly by ‘dy’. Since ‘y’ depends on ‘x’, it is crucial to recognize that both ‘u’ and ‘v’ also depend on ‘x’. Hence, when ‘x’ increases by ‘dx’, ‘y’ increases by ‘dy’, while ‘u’ and ‘v’ increase by ‘du’ and ‘dv’, respectively. This leads us to the following equation:

y + dy = (u + du) + (v + dv)

Chapter 2: Deriving the Sum and Difference Rules

Now that we have a workable equation, we can continue with our established procedures:

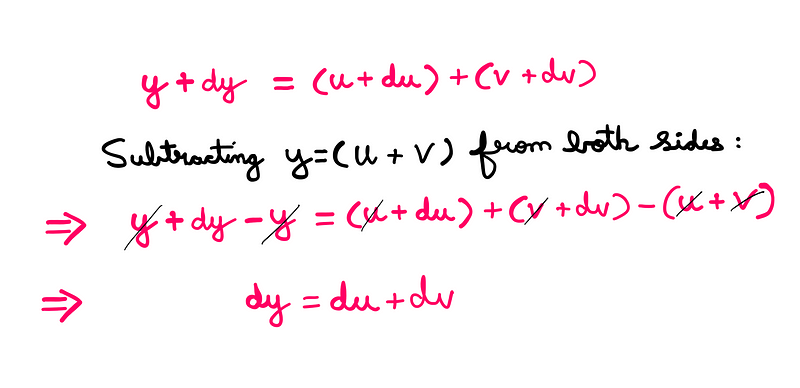
By dividing through by ‘dx’, we derive the desired derivative:

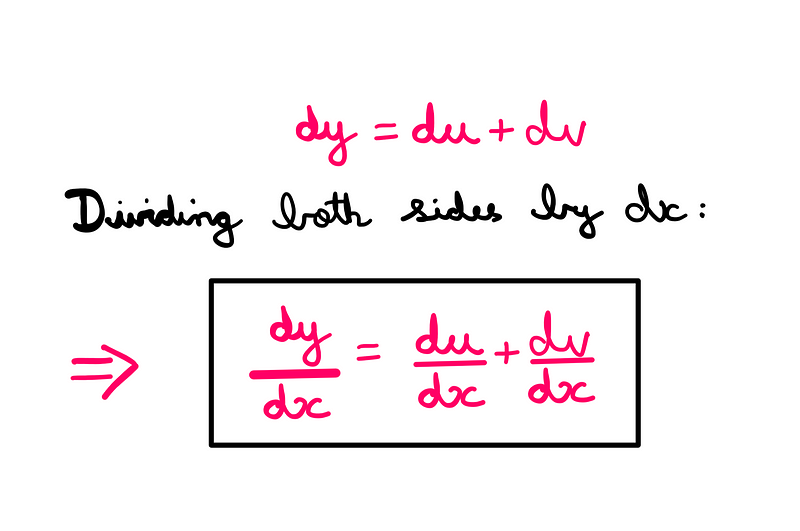
Thus, we have established a fundamental understanding of why the sum rule is valid. Implicitly, this also introduces the difference rule. If you’re unsure about the connection, don’t worry—let’s explore practical examples.

Examples of Applying the Sum and Difference Rules

We’ll begin with a straightforward application of the sum rule before moving on to the difference rule. Consider these functions:

u = 5x²

v = 3x

y = u + v

To find the derivative of ‘y’ with respect to ‘x’, we can apply the previously discussed power rule to differentiate ‘u’ and ‘v’, then use the sum rule to determine (dy/dx):

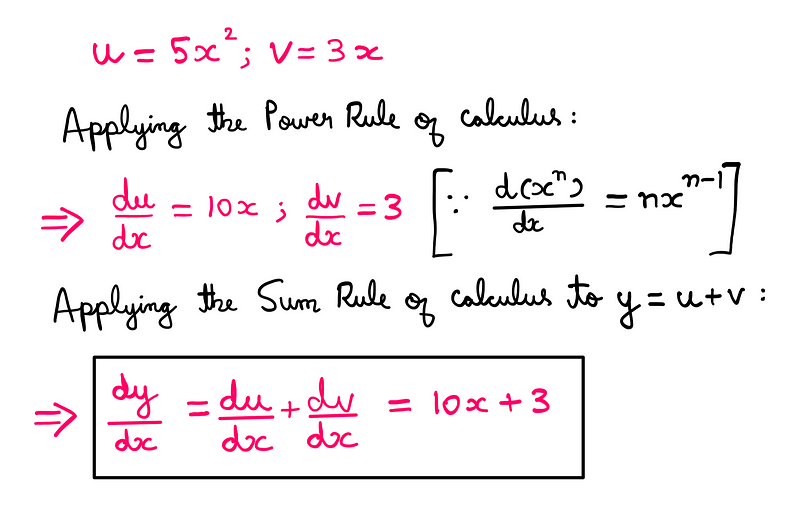
This example clearly demonstrates the sum rule’s functionality. Next, let’s turn our attention to the difference rule, which is a logical extension. Consider the following functions:

u = 5x²

v = 3x

z = u - v

To differentiate ‘z’ with respect to ‘x’, we apply the difference rule:

dz/dx = du/dx - dv/dx

To clarify how this works, we can reframe our original function as:

z = u - v = u + (-v)

When we apply the sum rule here, we arrive at the difference rule’s result:

dz/dx = du/dx + d(-v)/dx = du/dx - dv/dx = 10x - 3

Final Thoughts

As previously highlighted, the objective is to comprehend the reasoning behind these calculus principles. If you feel that we are merely revisiting basic concepts, remember that we are establishing the foundational building blocks for more complex topics ahead.

In future entries, we will delve into the product rule and the quotient rule. For a comprehensive overview of my work, please visit my about page.

If you wish to support the creation of future content, consider contributing on Patreon.

Reference and credit: Silvanus Thompson.

Read the original essay [here](link_to_original).

The first video, titled "Sum & Difference Rule," provides an in-depth exploration of these fundamental differentiation rules.

The second video, "The Sum and Difference Rule for Derivatives," offers additional insights and practical examples related to these rules.