What Exactly Are Coordinates?

Coordinates are numerical representations that indicate the position of a point in space. They typically consist of two or three values, depending on the dimensional context. We designate a specific point as the "origin" and measure the distance of any other point from this reference. For example, in three-dimensional space, coordinates are denoted as (x, y, z), where x indicates horizontal placement, y signifies vertical placement, and z reveals depth. In this system, x, y, and z are orthogonally aligned, forming a three-dimensional orthogonal coordinate structure.

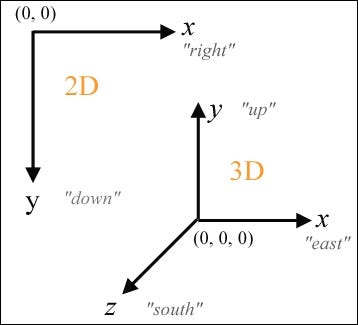
The Cartesian Coordinate System

Cartesian coordinates, which utilize x and y to represent points in a plane, are widely employed for describing various geometric forms and physical phenomena. However, in certain scenarios, polar coordinates may provide a more intuitive and practical framework.

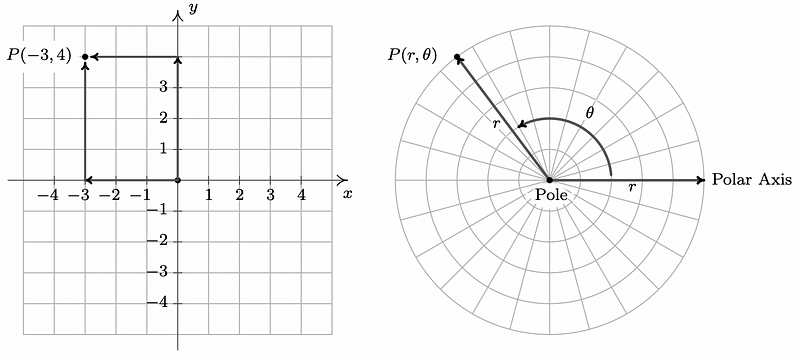
Named after the French mathematician René Descartes (1596–1650), Cartesian coordinates facilitate point representation in two-dimensional or three-dimensional spaces using numerical values. In a two-dimensional plane, points are expressed as (x, y), indicating their horizontal and vertical placements. The intersection of the x and y axes forms the origin, represented as (0, 0). For example, the point (3, 4) signifies a position 3 units right and 4 units up from the origin.

On the other hand, polar coordinates describe points through an angle and a distance from a fixed origin. In two-dimensional space, points are represented as (r, θ), where r is the distance from the origin and θ is the angle formed with a predetermined reference direction, often the positive x-axis.

Applications of Polar Coordinates

Polar coordinates are particularly advantageous in contexts involving circular or rotational symmetry, such as the case of spinning discs, spheres, or concentric circles like those surrounding Saturn.

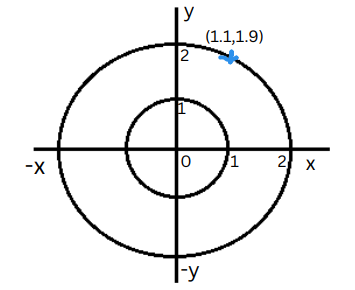
When employing Cartesian coordinates for circular configurations, it may not effectively capture the inherent symmetry. For example, using (r, θ) to represent points on a circle directly reveals their equal distance from the center, a crucial piece of information for solving related problems. In contrast, using Cartesian coordinates like (1.1, 1.9) might obscure this relationship.

Moreover, when analyzing planetary motion around a star, polar coordinates can elegantly express both the planet's distance from the star and the angle formed with a reference direction.

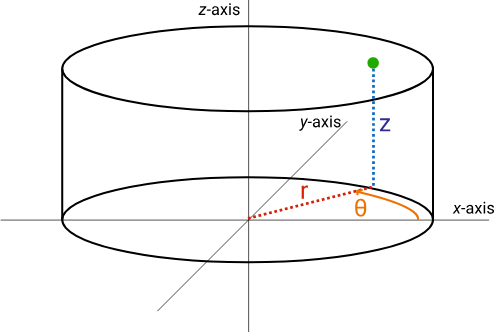
In scenarios featuring cylindrical symmetry, such as a bucket or a dumbbell, we can enhance our coordinate system by incorporating a z-axis from the Cartesian framework. This adjustment allows for the use of (r, θ, z) coordinates, known as cylindrical polar coordinates, facilitating a clear description of these objects.

Conversely, in cases of spherical symmetry, where any rotation about an axis through the origin yields the same shape, cylindrical coordinates may fall short. Here, introducing a second angle, φ, which measures the angle between the z-axis and the line connecting a point to the origin, allows for the description of spherical symmetric regions using spherical polar coordinates (r, θ, φ).

In conclusion, while Cartesian coordinates remain a powerful and versatile tool for representing numerous geometric shapes and physical systems, they can sometimes complicate equations and calculations. In such instances, polar coordinates may offer a more efficient and straightforward alternative, particularly for circular, spherical, and cylindrical configurations.

Thank you for engaging with this exploration. If you have any insights or feedback, feel free to share your thoughts in the comments section. Until next time, may your journey be filled with success and joy.

If you appreciate this content, please consider giving it a high rating or treating me to a coffee!