The Challenge of the Most Difficult Geometry Problem

One day, Max imagines himself tackling the most challenging geometry problem imaginable. In his daydream, his teacher assigns a bonus question intended as a joke.

Teacher: "I just put that up for fun. It’s likely the most difficult geometry equation in existence."

Student: "So, what’s the extra credit worth?"

Teacher: "Well, given that I’ve never seen anyone solve it, including my mentor at MIT, I can assure you that whoever cracks this will never have to touch another math book again."

The other students begin to chatter amongst themselves.

Teacher: "Max, are you going to give it a shot?"

Max: "Excuse me, did I hear my name?"

So, let’s check out the problem as it appears on the board!

Extra Credit on the Blackboard

Now, gather your math skills and attempt this problem for extra credit! If you manage to solve it, you’ll be free from ever needing to study math again!

Pause here, grab your pen and paper, and give it a shot. When you’re ready, continue reading for the solution!

What is an Ellipse?

Before we delve deeper, let’s clarify what an ellipse is. An ellipse is a two-dimensional curve defined by two focal points. For any point on the curve, the sum of the distances to these two focal points remains constant. Essentially, it broadens the definition of a circle, where both focal points coincide.

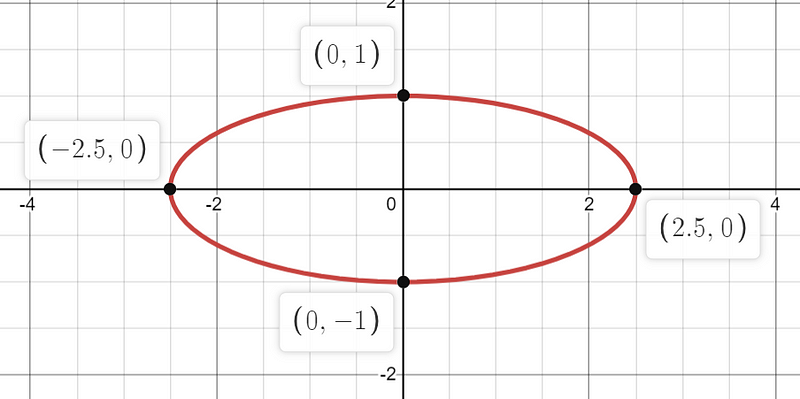
The equation of the ellipse is defined as follows:

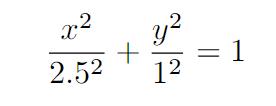
Here, 2.5 represents the semi-major axis, which is half of the longest diameter of the ellipse, denoted as 'a'. Similarly, 1 indicates the semi-minor axis, which is half of the shortest diameter, referred to as 'b'. The term 'e' represents the eccentricity, a value that indicates how much the ellipse deviates from being circular.

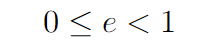
When e = 0, the shape is a perfect circle. With that background, let’s proceed to solve the problem for extra credit!

Solution to the Geometry Challenge

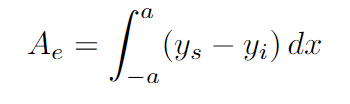
The integral we are dealing with shows the upper half of the ellipse.

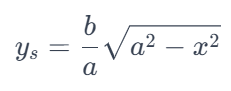
And this represents the lower half of the ellipse.

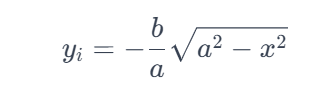
Due to the properties of definite integration, calculating the area for the lower half would yield a negative result.

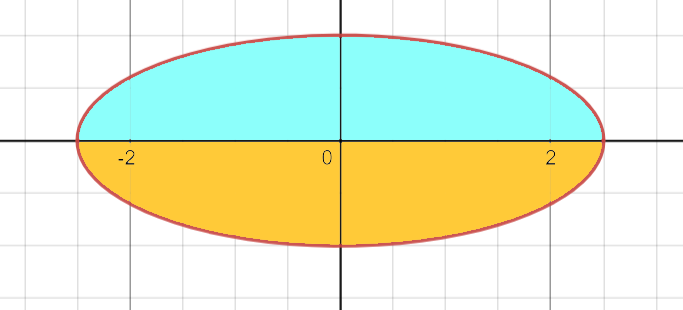
Thus, (ys - yi) effectively illustrates the vertical distance between the upper and lower parts of the ellipse at any x-coordinate. Recognizing that the ellipse is symmetric about the x-axis, this distance equals 2ys.

Consequently, the integral simplifies to:

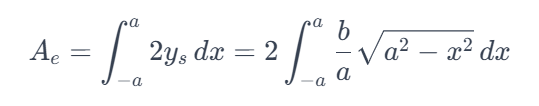
Now, we need to tackle this intricate integral! Here’s a tip: consider using trigonometric substitution…

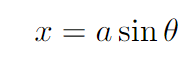
By differentiating both sides, we adjust the bounds on the integral as well.

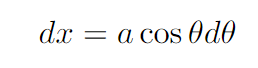
After substituting these values, we arrive at the following integral:

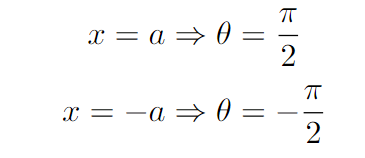
Ultimately, the definite integral of cos²(theta) d(theta) leads us to π/2.

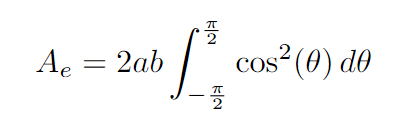
And this gives us the area formula for an ellipse.

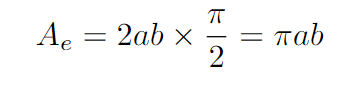
What a fascinating proof!

Did you manage to earn extra credit? Let me know in the comments; I’m excited to hear from you!

This video explores the hardest "easy" geometry problem, providing insights and explanations that can enhance your understanding of the concepts discussed.

The second video delves into the world's hardest geometry problem, featuring a unique perspective inspired by Wes Anderson's Rushmore.

Feel free to subscribe to my email list to stay updated on intriguing math puzzles and stories!

Math Puzzles

Find the best math puzzles on Medium, covering topics such as algebra, geometry, calculus, and number theory. Share this with friends and…

Thank you for reading! If you found this article helpful, don't forget to clap.

If you appreciate my work, consider buying me a coffee. Your support means a lot to me as I continue my writing journey. Happy Solving, Bella!